Em meados do século XV, os pilotos encontraram uma maneira de estimar a latitude do local em que se encontravam. Utilizaram um facto conhecido desde a Antiguidade: a altura dos astros depende da latitude. A partir desse momento, a medida da altura dos astros tornou-se essencial para a navegação e procuraram-se processos de aperfeiçoar o método de medida. Ao quadrante, ao astrolábio e à balestilha juntaram-se outros instrumentos. Pedro Nunes inventou o nónio, um processo de subdivisão das escalas, e ainda alguns instrumentos de concepção inovadora.

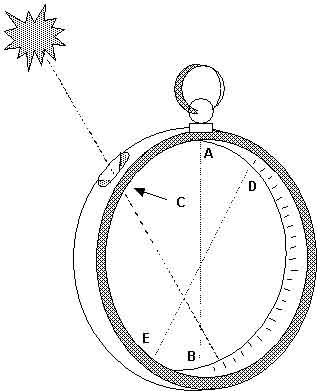
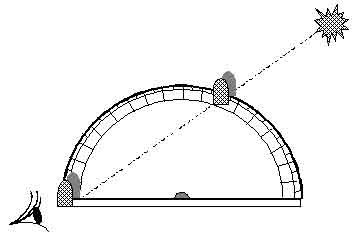
Para permitir um maior rigor na medição da altura do Sol, Pedro Nunes imaginou um instrumento que ficou conhecido como anel náutico, anel astronómico ou anel graduado. A sua ideia vem descrita numa obra que fez publicar em 1573 em Coimbra, De arte atque ratione navigandi libri duo, onde o matemático lhe chama apenas astrolábio, pois a sua forma é muito semelhante à de um astrolábio náutico a que se retire a cruzeta central.

O instrumento compunha-se simplesmente de um anel dotado de uma argola de suspensão que permitia mantê-lo na vertical. Possuía um orifício muito pequeno a 45º desse ponto de suspensão. Era alinhado de forma a deixar a luz do Sol passar por esse orifício e projectar-se sobre o interior do anel, que estava graduado. A altura do Sol era medida nessa escala.

Há várias imagens antigas desse instrumento, mas a primeira que se conhece com algum pormenor e que nesse particular indicia a sua construção e uso é a que Manuel Pimentel inseriu na sua obra Arte de Navegar, publicada em Lisboa em 1712. As ilustrações anteriores que apareceram, tanto a original de Pedro Nunes de 1573 como a reprodução seguinte que se conhece, do Regimiento de Navigación do espanhol André Garcia de Cespedes, publicado em Madrid em 1606, são muito esquemáticas.

O anel náutico permitia ler a altura do Sol na escala graduada marcada no interior do anel, no arco EBD. A luz do Sol passava através do orifício C e projectava-se nessa escala. Com o anel suspenso pela argola A, a linha AB mantinha-se na vertical. Desta forma, se o Sol se encontrasse no zénite a luz seria projectada no ponto E, marcando a altura de 90º. Se se encontrasse na linha de horizonte a sua luz seria projectada no ponto D, marcando a altura de 0º. De notar que, assim, o ponto de projecção percorre 180º enquanto a altura do Sol apenas varia de 90º. Esta é a grande vantagem teórica do instrumento, pois cada grau de altura corresponde a dois graus no aparelho, o que deveria permitir um rigor duplo. (Desenho da prof. Susana Nápoles.)

Pedro Nunes dá várias indicações práticas para a construção do instrumento. Indica que o anel devia ter a espessura de «um dedo» (medida da época que equivale a pouco menos de 2 cm), e insiste em que o orifício devia ter o menor diâmetro possível. Explica que era necessário «cortar uma certa porção em forma de ângulo», marcado na gravura GCF, de forma a que a luz pudesse passar pelo orifício, qualquer que fosse a posição do Sol. E diz que, «por causa daquela porção de metal que foi retirada do instrumento, o mesmo círculo fica menos pesado» desse lado; para o manter exactamente na vertical seria pois necessário compensar esse perca de peso e «retirar a mesma quantidade de metal da outra parte».

A vantagem do anel náutico sobre um astrolábio normal seria, segundo Nunes, que as marcas na escala EBD «são neste instrumento duas vezes maiores do que seriam se sobre o centro rodasse uma alidade, como vemos no astrolábio habitual».

O anel náutico baseia-se numa propriedade geométrica que Euclides demonstra na proposição 20 do livro III dos seus Elementos e que Nunes expressamente refere dizendo que o ângulo «que está na circunferência do círculo contém um arco duplo do que tem vértice no centro». Em linguagem moderna, dir-se-á que o ângulo ao centro, isto é, com vértice no centro do astrolábio, é duplo do ângulo inscrito, isto é, com vértice no ponto C.

O anel náutico representa uma aplicação engenhosa da geometria e foi louvado por alguns estudiosos da época. No entanto, tinha um inconveniente que tornava ilusória a vantagem imaginada por Nunes: por mais diminuto que fosse o orifício, a luz projectada pelo Sol no interior do arco graduado nunca se podia reduzir a um ponto, dado que a nossa estrela não nos aparece como um ponto, mas sim como um disco. Como esse disco tem um diâmetro de cerca de meio grau, a imagem projectada ocupa pelo menos meio grau, o que reduz a precisão do instrumento. Esse inconveniente já não existiria no caso de se pretender medir a altura de estrelas, mas a luminosidade destas não é suficientemente forte para se projectar visivelmente através no arco graduado.

Esquema de funcionamento do semicírculo graduado. Neste instrumento, a altura do astro corresponde ao ângulo entre a base e a orientação da mira móvel e é medida na escala do semicírculo. Construindo a mira com precisão, tira-se partido da ideia inicial de Pedro Nunes pois cada grau de altura corresponde a dois graus do ângulo ao centro. (Desenho da prof. Susana Nápoles.)

No invento de Nunes parece vislumbrar-se uma característica comum a muitos dos seus trabalhos. O cosmógrafopossui um domínio da geometria e da matemática e um extraordinário espírito criativo que o leva a conceber instrumentos imaginativos e potencialmente úteis. No entanto, admite-se que a sua inexperiência na utilização de instrumentos leve a que as suas propostas não sejam tão eficazes como imaginava. Muitas ideias base de Pedro Nunes, no entanto, podem e vêm mais tarde a ter aplicações frutuosas. Assim aconteceu com este instrumento, que não se revelou útil à navegação, mas que deu origem a vários outros, entre os quais o chamado semicírculo graduado. Este último, estava dotado de uma mira móvel que permitia apontar para uma estrela e ler a sua altura numa escala semelhante à do anel náutico. A ideia da duplicação do ângulo na escala de medida revelou-se, afinal, uma ideia frutuosa.

Nuno Crato