Na civilização muçulmana, o estudo de Geometria mais antigo que se conhece é da autoria do célebre Muhammad iben Muça al-Khuarizmi (c. 780–850), matemático de origem persa que se conta entre os primeiros membros da Casa da Sabedoria (Bait al-Hikma) de Bagdade. Em al-Khuarizmi, a geometria aparece ao serviço das demonstrações algébricas, de forma semelhante ao que se passou durante muitos séculos posteriores. Os geómetras islâmicos, no entanto, foram muito mais longe e foram precursores directos de Pedro Nunes no estudo de alguns problemas de trigonometria esférica, ramo da geometria que se viria a tornar um instrumento crucial da navegação.

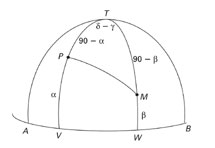
Os islamitas estudaram os ângulos de triângulos sobre a superfície da esfera terrestre, motivados por um problema religioso de implicações geométricas interessantes. Esse problema é o da qibla, ou seja, o da determinação da direcção de Meca. Como se sabe, os muçulmanos devem rezar orientados para essa cidade sagrada, o que levanta o problema da determinação rigorosa da direcção dessa cidade num ponto dado do globo. O problema é fácil de resolver com precisão razoável nas proximidades de Meca, mas passou a ser difícil quando a civilização islâmica se estendeu à península Ibérica, ao Atlas africano e a outros locais afastados da Arábia. Al-Biruni criou um método rigoroso de determinação da direcção de Meca dadas as coordenadas do local onde o crente se encontre. O problema veio a ser retomado mais tarde por Pedro Nunes no contexto da navegação. O matemático português estava interessado em determinar a direcção que o navio deveria tomar para chegar ao porto de destino. O seu problema generaliza o da qibla, tornando-o num problema dinâmico. Com efeito, a rota mais curta, sobre um círculo máximo, não é em geral dada por uma direcção cardeal constante, sendo preciso ajustá-la durante a viagem para manter o navio nesse trajecto óptimo. Essa rota mais curta sobre o círculo máximo veio a ser conhecida como ortodrómica, e não é a de direcção cardeal constante, mais tarde conhecida como loxodrómica. A distinção entre as duas rotas constitui, como se sabe, um dos maiores feitos de Pedro Nunes.

Os problemas de trigonometria esférica têm interesse para a náutica teórica, mas os Árabes legaram ainda ao Ocidente, nomeadamente aos Ibéricos, vários conhecimentos e técnicas de navegação que se tornaram imprescindíveis para as Descobertas. Contam-se aí técnicas como a vela latina (triangular), conhecimentos astronómicos para a determinação de coordenadas, nomeadamente tabelas de alturas do Sol, cartas náuticas e diversos conhecimentos geográficos. Mesmo depois de os Portugueses terem conseguido dobrar as costas de África, foi-lhes útil a ajuda de um piloto árabe para navegar no Índico. Como Camões relata (Lusíadas, VI, 5):