|
|
|||||||||||||||
|
|
|||||||||||||||
|
Pedro Nunes, Mercator e Escher Tudo isto pode parecer simples e evidente, mas demorou muito tempo a que os navegadores o entendessem. O primeiro a percebê-lo em toda a sua extensão foi Pedro Nunes (1502-1579). O cosmógrafo real deparou-se de facto, com o problema inverso, que é um problema mais difícil: será que, para se viajar entre dois pontos, é conveniente tomar sempre a mesma direcção? O problema foi-lhe sugerido por Martim Afonso de Sousa, fundador das primeiras colónias que Portugal teve no Brasil. Querendo vir do Rio da Prata para Lisboa, verificou que deslocar-se para leste não bastava e que precisava de se deslocar também para norte. Mais importante, não era fácil perceber qual era a direcção exacta em que deveria viajar. O génio de Pedro Nunes consiste em ter distinguido claramente duas possíveis trajectórias para um barco no mar alto. Uma seria a trajectória de distância mínima entre dois pontos, correspondendo a um arco de círculo máximo - é a chamada ortodromia. Outra, seria a trajectória seguida por um barco que mantivesse sempre a mesma orientação em relação aos pontos cardeais - é a chamada linha de rumo, mais tarde conhecida como loxodromia. Só em casos muito especiais é que as duas trajectórias coincidem: quando se viaja ao longo do Equador, de leste para oeste ou de oeste para leste, ou quando se viaja ao longo de um meridiano, de norte para sul ou de sul para norte. Em todos os outros casos, as duas trajectórias não coincidem. Para seguir a trajectória mínima entre Lisboa e Nova Iorque, os aviões não seguem uma linha de rumo, mudam constantemente de orientação cardeal, para poderem seguir um arco de círculo máximo. Ao descobrir a linha de rumo, Pedro Nunes provou também que um barco que, hipoteticamente, num planeta completamente coberto de água, seguisse sempre uma mesma direcção cardeal, acabaria por não regressar ao mesmo lugar, como na altura se pensava, mas seguiria uma espiral infinita, dita espiral loxodrómica, aproximando-se de um dos pólos, mas só o alcançando após um número infinito de voltas. Os desenhos mais espectaculares de espirais loxodrómicas são, sem dúvida, os de Mauritus Cornelius Escher (1898-1972). Em 1958, Escher criou alguns desenhos de esferas com espirais, ao que parece sem consciência do seu profundo significado histórico e geométrico. A gravura que aqui reproduzimos chama-se «Bolspiralen», espirais esféricas, e é um dos seus mais belos exemplos. Trata-se de uma gravura de madeira em quatro blocos, cada um para sua cor, com 32 cm de diâmetro. Podemos imaginar um barco que decida seguir sempre um rumo a um ângulo de cerca de 60 graus com a direcção norte-sul. As espirais mostram o caminho seguido por tal barco. E mostram que o barco pode partir de sítios diferentes, que a sua trajectória convergirá. As faixas são mais largas perto do Equador e tornam-se mais estreitas perto dos pólos. O grande problema da construção de mapas planos é o aparecimento de deformações inevitáveis. Tal como ao calcar uma casca de laranja sobre uma mesa, esta se fractura e deforma, assim os fazedores de mapas têm de deformar a geometria do globo para poder reproduzir no plano uma superfície esférica. As deformações não são graves quando se trata de áreas reduzidas. Mas o mundo tinha-se tornado maior com as viagens dos Descobrimentos e começavam a fazer-se mapas de continentes e oceanos, que eram necessários para as navegações. O mapa de Mercator é o que se chama um mapa conforme, pois preserva a direcção entre quaisquer dois pontos do globo. Mas o mapa de Mercator introduz distorções inevitáveis, que moldaram a nossa intuição geográfica. Nesse mapa, a Gronelândia parece enorme, maior que a América do Sul, quando, afinal, esta tem uma área nove vezes maior. E o mapa engana também os viajantes modernos, que ainda hoje se espantam com os caminhos que os aviões seguem. |
|||||||||||||||
 |
|||||||||||||||
|
|
|||||||||||||||
| © Instituto Camões 2003 | |||||||||||||||
 QUEM viaja de Lisboa para Nova Iorque costuma aproximar-se da costa norte-americana pelo menos uma hora antes da chegada ao destino. Nessa hora, observa a costa recortada do Estado do Massachusetts, a ilha Martha's Vineyard e outros destinos turísticos. Sobrevoa depois Long Island e as suas praias, viajando de norte para sul em direcção à cidade de Nova Iorque. Olhando para o mapa, parece que o avião fez um grande desvio e que, em vez de voar a direito sobre o Atlântico, preferiu encontrar o Novo Mundo a norte, onde pela primeira vez os portugueses o abordaram, e descer depois para o seu destino.
QUEM viaja de Lisboa para Nova Iorque costuma aproximar-se da costa norte-americana pelo menos uma hora antes da chegada ao destino. Nessa hora, observa a costa recortada do Estado do Massachusetts, a ilha Martha's Vineyard e outros destinos turísticos. Sobrevoa depois Long Island e as suas praias, viajando de norte para sul em direcção à cidade de Nova Iorque. Olhando para o mapa, parece que o avião fez um grande desvio e que, em vez de voar a direito sobre o Atlântico, preferiu encontrar o Novo Mundo a norte, onde pela primeira vez os portugueses o abordaram, e descer depois para o seu destino.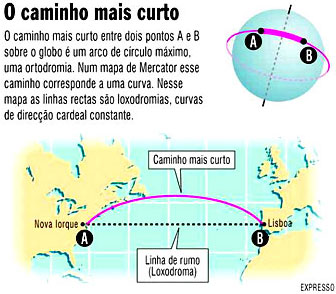 Além de mostrar aos navegadores o caminho que se segue quando se toma um rumo cardeal constante, as loxodrómicas de Pedro Nunes tiveram um efeito decisivo na nossa visão do mundo. Elas determinaram a maneira como os mapas começaram a ser feitos e criaram a visão que hoje temos dos continentes. O nosso matemático teve a intuição de que os antigos mapas portulanos tinham de ser refeitos, mas foi Gerardus Mercator (1512-1594) quem haveria de originar uma revolução em cartografia, com base na descoberta de Pedro Nunes.
Além de mostrar aos navegadores o caminho que se segue quando se toma um rumo cardeal constante, as loxodrómicas de Pedro Nunes tiveram um efeito decisivo na nossa visão do mundo. Elas determinaram a maneira como os mapas começaram a ser feitos e criaram a visão que hoje temos dos continentes. O nosso matemático teve a intuição de que os antigos mapas portulanos tinham de ser refeitos, mas foi Gerardus Mercator (1512-1594) quem haveria de originar uma revolução em cartografia, com base na descoberta de Pedro Nunes.